Doğanın kesirli (fraktal) geometrisi (2)
İlk bakıldığında kaotik yani karmaşık gibi görülen evrendeki/doğadaki oluşumların aslında yapısında sadelik ve basitlik barındırdığını söyleyebiliriz. Her ne kadar kaotik durumda yani kaosta düzensizlik (entropi) artsa da sistemin tümü ya da en küçük parçası kendi içerisinde belli bir düzene sahiptir. Kısaca, kaos düzensizliğin düzeni şeklinde tanımlanabilir [10,11].
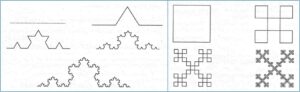
![]() Fraktal geometrinin elde edilmesine örnekler [3]
Fraktal geometrinin elde edilmesine örnekler [3]
Fraktal geometri ortaya çıktıktan sonra bilim adamları fraktal boyut fikrine de yönelmişlerdir. Bilindiği üzere, üç boyutlu bir uzayda yaşamaktayız ve düzlemin boyutunun iki, doğrununkinin bir ve noktanınkinin ise sıfır olduğu herkes tarafından kabul edilmektedir. Fraktal geometrinin fikir babası olan Mandelbrot’a bir iplik yumağının boyutu sorulduğunda ise yanıtı “Bu sizin bakış açınıza bağlı bir olay” şeklinde olmuştur. Uzaktan bakıldığında yumak bir noktadan ibarettir, yani boyutu sıfırdır. Daha yakından yapılan gözlemlerde yumak, yüzeyinde düzensizlikler bulunan bir küre gibidir. Boyut sayısı üçe çıkmıştır. Daha yakından bakıldığında yumağı oluşturan tek boyutlu iplik ayrık olarak gözlemlenebilir [13]. Bu noktada fraktal boyut kavramına yönelmemiz gerekmektedir. Fraktal yani kesirli boyut açıklanması zor bir kavramdır. Öklid boyutunun tersine fraktal boyut kesirli bir sayı ile ifade edilir ve fraktal bir eğri yani belli değişkenleri olan bir fonksiyonla ifade edilebilir. Bu eğrinin çevre uzunluğu ise her aşamada 4/3 oranında büyür [3,9].
Fraktal geometri istatistik, bilgisayar programcılığı, mimari, fizyoloji gibi birçok yerde kullanılabilmektedir. Örneğin gökada (yıldız takımları) kümelerinin evrendeki dağılımlarının saptanmasında, astroidlerin incelenmesinde [14] veya bilgisayarda engebeli dağlık arazilerin gerçeğine benzer görüntülerinin oluşturulmasında…[3,4,9,10]
 Bilgisayar programlarıyla elde edilen fraktal örnekler [15]
Bilgisayar programlarıyla elde edilen fraktal örnekler [15]
Fraktal şekiller doğal bir süreç sonunda ortaya çıkmaktadır. Başka bir deyişle doğa bir çeşit kendiliğinden ölçek değişmezliği gösteren yapılar oluşturmaktadır. Doğadaki mevcut bu sürecin bilim adamları tarafından modellendirilmesi fraktal şekillerin nasıl oluştuğunu anlamamıza yardım etmektedir [16].
 Mimaride fraktaller [17]
Mimaride fraktaller [17]
Aslında doğaya baktığımızda mevcut yapının kesin bir şekilde, sadece Öklid geometriye ya da sadece fraktal geometriye uyduğunu söylememiz pek de doğru olmaz. Bu durum çok basit bir örnekle açıklanabilir. Doğadaki tuz yataklarındaki tuz (NaCl) kütleleri şekilsiz, girintili çıkıntılı bir yapı sergiler. Bulunduğumuz yerden bakıldığında bu yapının fraktal geometriye uyduğu söylenebilir. Fakat X-ışını kristalografisi ile daha yakından bakıldığında örneğin kristal yapısının Öklid geometrisiyle betimlenen yüzey merkezli kübik bir kristal yapıya sahip olduğu görülür.
 Tuz (NaCl) kütlesi ve kristal yapısı
Tuz (NaCl) kütlesi ve kristal yapısı
Fraktal geometri yaşamı kavramamızı ve etrafımızda var olan çeşitliği fark etmemizi sağlar [18]. Fakat Öklid geometrisi de içinde bulunduğumuz uzayın belli bir kısmı için mükemmel bir gösterim sağlayabilir. Kısacası hangi referans siteminde hangi geometrinin geçerli olduğunun tespiti önemlidir [19]. Bunların yanı sıra, Öklid olsun veya olmasın doğayı eksponansiyel ifade ile tanımlayarak, bu anlam kargaşasını da en basite indirgenebileceği rahatlıkla söylenebilir. Bu durumda türev veya integral hesapları her iki geometri için de doğru sonuç verecektir. Kısaca, doğa işleyişi bakımından eksponansiyel bir yapı sergileyerek, çok değerli bir bilim insanımızın da dediği gibi toprağa bakan lâle yani Gauss eğrisine uyar.

Prof. Dr. Özden Aslan Çataltepe
Kaynaklar:
[13]http://tr.wikipedia.org/wiki/Fraktal
[14]http://ti.arc.nasa.gov/publications/pdf/iafa.pdf
[15] http://www.musl.org/images/fractal_hand.jpg
[16] D. R. Morse, J. H. Lawton, M. M. Dodson, M. H. Williamson, Fractal dimension of vegetation and the distribution of arthropod body lengths, Nature 314, 731 – 733, 25 April 1985
[17]http://myweb.lmu.edu/pharris/WTmed%20liftoff%20towers.jpg
[18]Şahin Koçak, Fraktaller, Matematik Dünyası, Bahar, Syf: 66-67, 2004
[19] http://www.people.umass.edu/partee/409/Appendix%20non-Euclidean.pdf

