Doğanın kesirli (fraktal) geometrisi (1)

Doğada gizli olan altın oranın bir tam sayıya eşit olmaması, aksine sürekli olarak 1,618’den sonra değişen farklı uzantılara sahip olması nedeniyle doğada kesirli (fraktal) bir yapı ortaya çıkar. Örneğin, bulutlara, dağlara, nehirlere veya insan vücudundaki sistemlere, kısacası doğadaki oluşumlara baktığımızda bunları bilinen matematiksel eğriler ile yani daire, dikdörtgen, elips, silindir, küre gibi düzgün Öklidyen (kare, dikdörtgen, daire gibi düzenli geometrik şekillere Öklidyen şekiller denir) şekillerle ifade etmenin mümkün olmayacağını görürüz. Doğadaki bu tarz oluşumlar veya şekiller fraktal yani kesirli geometrilerle birlikte incelenebilmektedir [1-4]. 

Bilindiği gibi doğada en çok görülen yapılaşma sarmallardır ve doğada bizi altın oran kavramına götüren Fibonacci (Fibonaçi) serisine eşdeğer birçok sarmal yapı mevcuttur. Fibonacci serisine eşdeğer bu sarmal yapılar Fibonacci sarmalı olarak adlandırılırlar. Doğada hem dinamik hem de durağan sarmallar gözlenebilir; örneğin tayfunlar, saman yolu, çam kozalakları, DNA sarmalı gibi. En ilginçleri arasında logaritmik sarmallar vardır. Bu yapılaşmaların büyümesi eksponansiyel formda olur. (Matematikte e sayısı üssü veya üstel anlamında kullanılan terimdir. e sayısı veya Euler sayısı ise sabit reel bir sayı olup, yaklaşık değeri 2,718281828…’dir.) [5]. Aynı şekilde doğadaki radyoaktif bozunma gibi fiziksel süreçlerde eksponansiyel dağılıma örnek verilebilir. İnsanlığın bilgi ve beceri dağarcığı gibi sosyal gelişmeler de eksponansiyel bir değişim göstermektedir [6]. 

ahtapotlar ailesinden olan ve şekli eski çağlardan beri değişmemiş ve
Büyük Okyanus’un derinlerde yaşayan kabuklu bir canlı olan nautilus

Tüm bu bilgiler ışığında, özellikle doğadaki fiziksel olaylara ve görsel olarak logaritmik algılama özelliklerimizi göz önüne alarak etrafımızda meydana gelen değişiklikleri tam anlamıyla fark edebiliyor muyuz sorusu gündeme gelebilir. Farkındalık sürecine geçmeden önce fraktal kavramının tarihsel gelişimi hakkında bilgi vermek daha yararlı olacaktır.

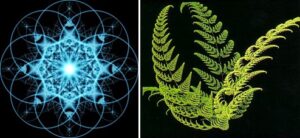
bilgisayar programlarıyla elde edilen fraktal örnekler

Fraktal kavramının temel aldığı fikirler çok daha önceleri G.Cantor, G.Peano, D.Hilbert, H.Koch, W.Serpinski gibi matematikçiler tarafından ortaya atılsa da, bu fikirlerin ilk defa bir araya getirilmesi 1975 yılında Polonya asıllı bir matematikçi olan Beneoit B. Mandelbrot tarafından olmuştur [7,8]. Mandelbrot’un kesirli geometri olarak tanımladığı evren; pürüzlü, girintili çıkıntılı, bükük bir evrendir. Fraktal geometride bir cismi oluşturan parçalar ya da bileşenler cismin tamamına benzemektedir. Kısaca, düzensiz ayrıntılar, desenler daha da küçülen ölçeklerde kendini tekrarlamaktadır [3,4,9-11]. Fraktal teriminin kökenine baktığımızda ise Latince “fractus” sözcüğünden geldiğini görmekteyiz ve anlam olarak da parçalara ayrılmış veya kırılmış demektir [10].

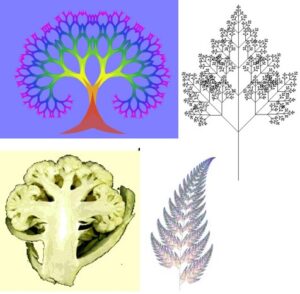
doğadaki fraktal yapılara örnekler [12]

Fraktal geometrisi, Öklid geometrisinde mevcut olan belirli karakteristik büyüklüklerden (örneğin dairenin yarıçapı) daha fazla karakteristiğe sahiptir ve ölçek ya da büyüklüklerden bağımsızdır [3]. Tüm bu bilgiler ışığında doğadaki oluşumlara bakarak birçok fraktal örneği verebiliriz. Kar taneleri, ağaçlar, geniş alanlara yayılı nehirler, sinir ağları gibi sistemler fraktal bir yapı sergilerler. Daha da ayrıntıya girersek, bu konu hakkında daha geniş bir fikre sahip olabiliriz. Bir ağaca baktığımızda ağacın bir gövdeye, onun üzerinde birkaç ana dala, bu ana dalların üzerinde de ince dallara sahip olduğunu görürüz. Karmaşık bir yapı halinde görülen ağacın bir dalını kopardığımızda elimizde minyatür bir ağacın olduğunu fark ederiz. Benzer özellikler akciğerlerimizdeki bronş ve bronşcuklarımızda da mevcuttur. Daha da derinleştiğimizde mikroevren dediğimiz atom altı dünyanın, makroevren ile aynı olduğunu anlarız [3,4,10].

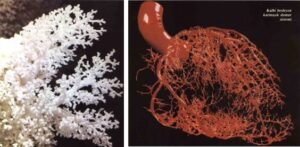
akciğerlerin hava yolları (bronşlar) ve kalbi besleyen karmaşık damar sistemi

 

Devam edecek…

Prof. Dr. Özden Aslan Çataltepe

Dinlemek için tıklayın

 

Kaynaklar:
[1]Gürkan Öztürk, Kaos: Düzensizliğin Düzeni, Bilim ve Teknik, Ağustos 1990, syf 8, Sayı 273
[2]Ayşe Erzan, Doğadaki Fraktallar, Bilim ve Teknik, Nisan 1998, syf 34, sayı 365
[3]Ünal Ufuktepe ve İsmail Aslan, Fraktal Geometriden Bir Kesit, Matematik Dünyası-C:11-s:1-Syf:14-2002
[4]www.iyte.edu.tr/~acarsavaci/Fraktal%20Geometri.doc
[5]http://nucleus.istanbul.edu.tr/~cfe/birinci/mak2/index.html
[6]İsmet Gedik, Karadeniz Teknik Üniversitesi, Jeoloji Mühendisliği Bölümü, Dünyanın Oluşumundan İnsanlığın Gelişimine: Değişimler ve Dönüşümler, Us-Jeoloji Müh., Sayı 52, Mayıs 1998, Syf 75-139.
[7] B. Mandelbrot,  The Fractal Geometry of Nature, W. H. Freeman. San Francisco, 1982.
[8]Deniz Gündüz, Fraktallar Dünyasında Küçük Bir Gezinti, Bilim ve Teknik, Nisan 1998, syf40, Sayı365
[9]http://www.metu.edu.tr/~e128393/son10.html
[10]http://www.matematikkulubu.org/modules.php?name=News&file=article&sid=510
[11]http://goto.bilkent.edu.tr/gunce/forum_posts.asp?TID=948
[12]http://www.fractal.org/Fractal-tree-scaffold.htm